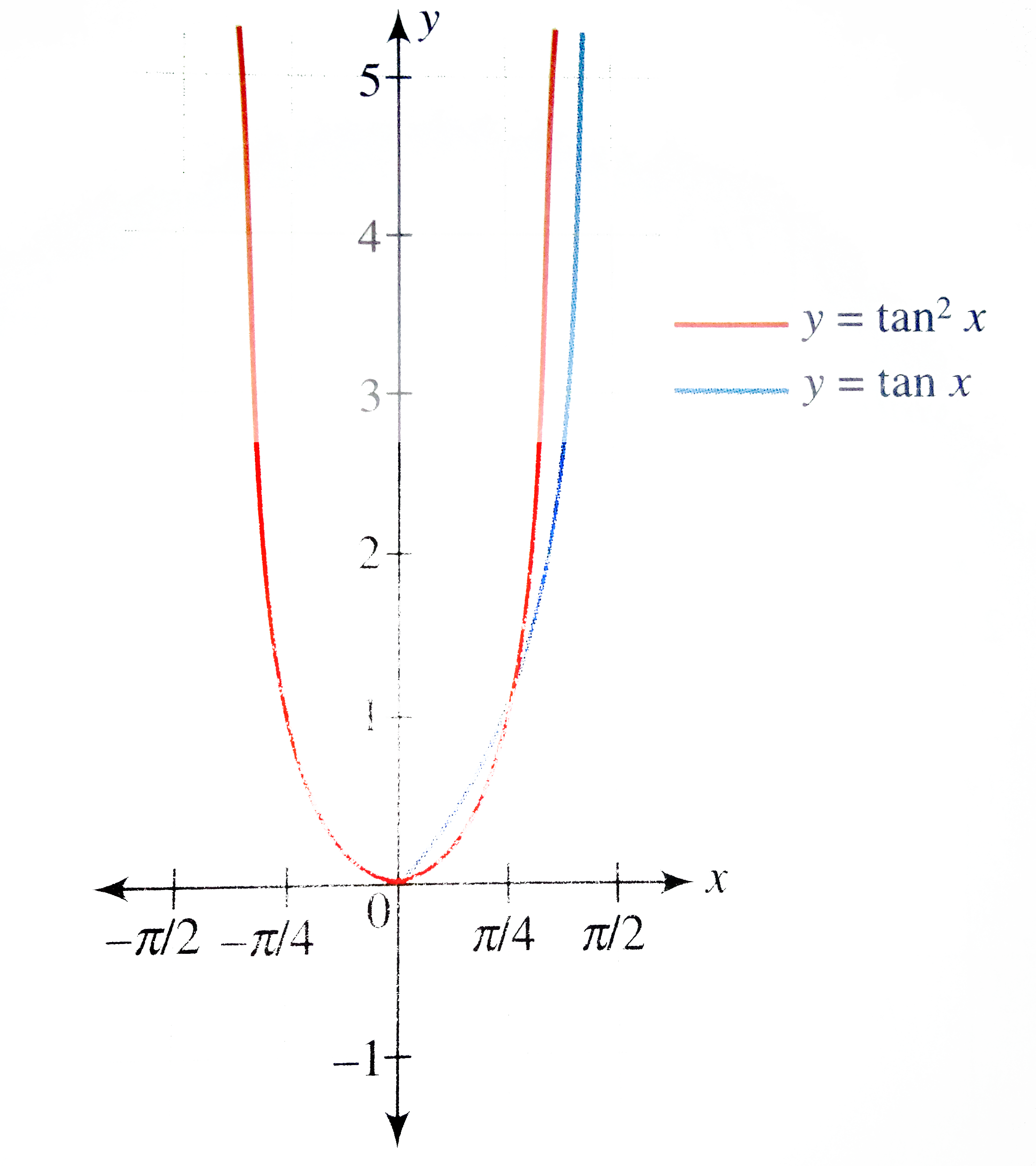
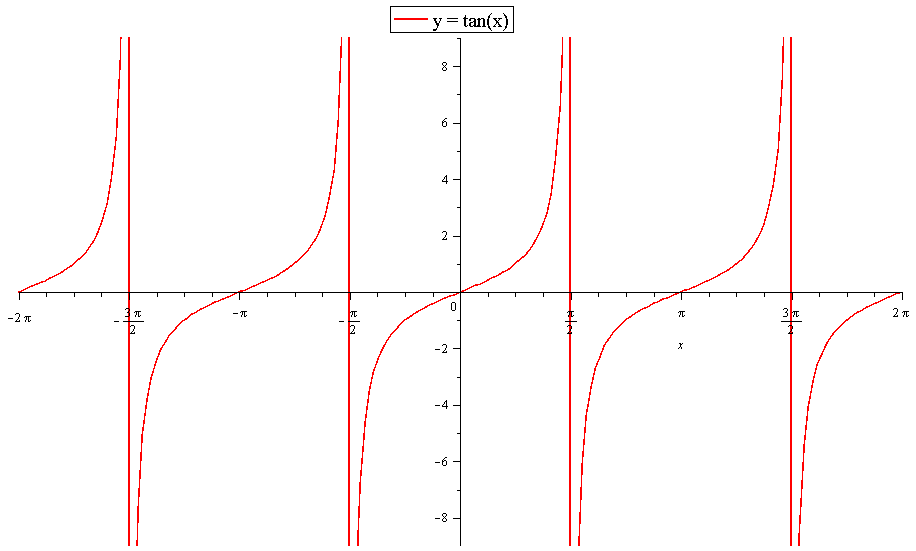
We show these in the graph below with dashed lines Since the cotangent is the reciprocal of the tangent, latex\cot x/latex has vertical asymptotes at all values of x where latex\tan x=0/latex , and latex\cot x=0/latex at all values of x where tan x has its vertical asymptotesIn mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many othersIn fact ,there are infinite solutions, you can realise it easily,here x=tanx ,so let y=x(1) and y=tanx(2) ,for (1) ,you'll get a straight line and for (2) ,it's tan curve,the intersection of both graph will give you solution points,as (1) and (2
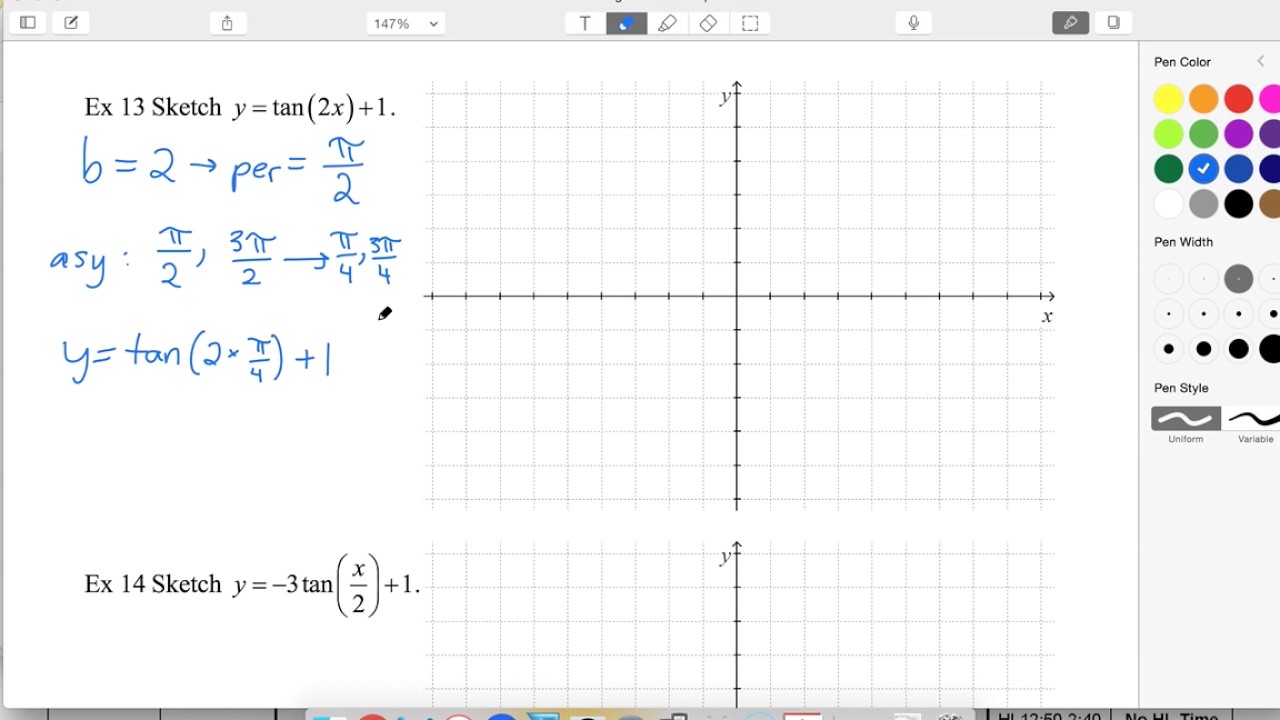
01 Ex13 Sketch Y Tan 2x 1 Youtube
Y=tan(2x) graph
Y=tan(2x) graph-3/2/13Y = TAN X 5 Changing Trigonometric GraphsYou should know how the following graphs differ from the basictrigonometric graphsY= 2 SIN X The 2 in front of the sin x changes the "amplitude" of the graph 6 Y = 5 COS XAs expected the amplitude of the graph is now 5 Hence thegraph has a maximum value of 5 and a minimum value of –5 7Professionals For math, science, nutrition, history


Tangent Cotangent Secant And Cosecant Graphs Mathbitsnotebook Ccss Math
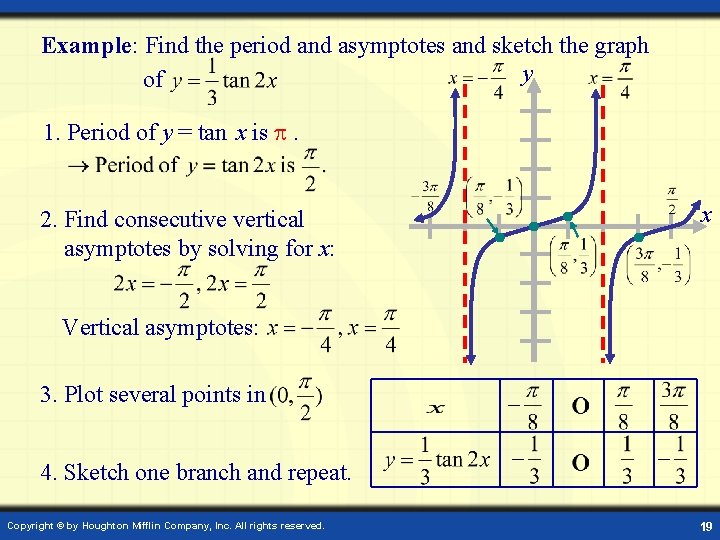
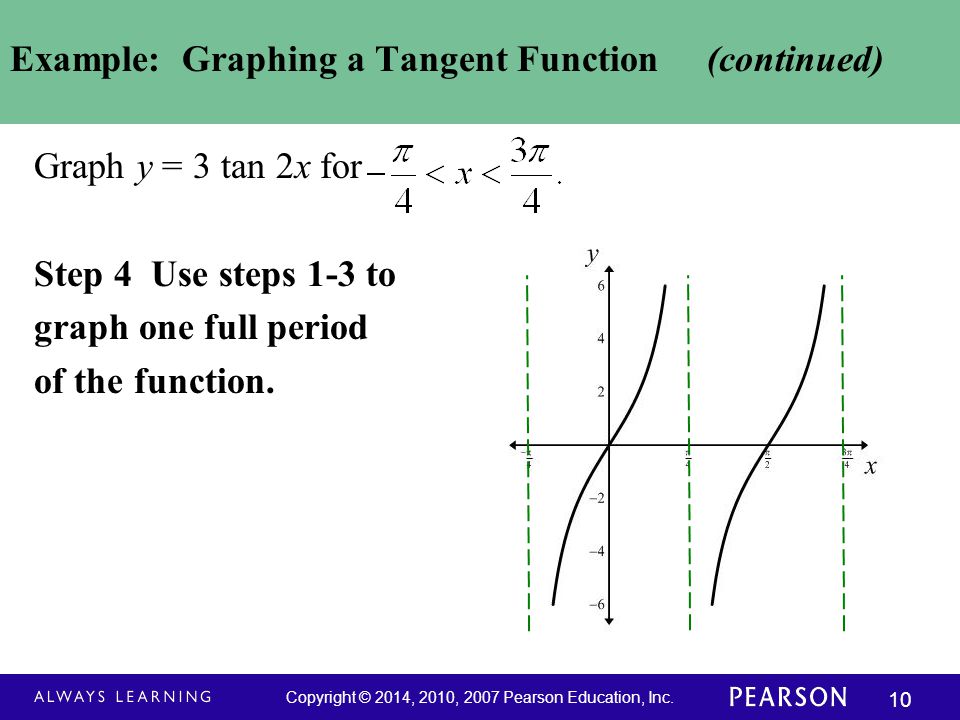
X^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \leAnswer to Find the period y = tan(2x pi/2) Graph the function By signing up, you'll get thousands of stepbystep solutions to your homeworkFind the asymptotes Tap for more steps For any y = tan ( x) y = tan ( x), vertical asymptotes occur at x = π 2 n π x = π 2 n π, where n n is an integer Use the basic period for y = tan ( x) y = tan ( x), ( − π 2, π 2) ( π 2, π 2), to find the vertical asymptotes for y = 4 tan ( x) y = 4 tan ( x)
2 π } Thus, it has been defined for − 2 π <Function ln(tan2x) is even Has periodicity π so I will be graphing only the interval ( − π 2, π 2) f '(x) = 1 tan2x ⋅ 2tanx ⋅ 1 cos2x f '(x) = cos2x sin2x ⋅ 2tanx ⋅ 1 cos2x f '(x) = 2tanx sin2x tanx = 0 ⇔ x = 0 x ∈ ( − π 2,0) ⇔ f '(x) <Online Graphing Calculator Plot your own SVG Math Graphs You can plot 2 functions, function 1 (in dark green) and function 2 (in magenta) Edit your functions and then click the Graph it button below To remove a graph, leave its text box blank
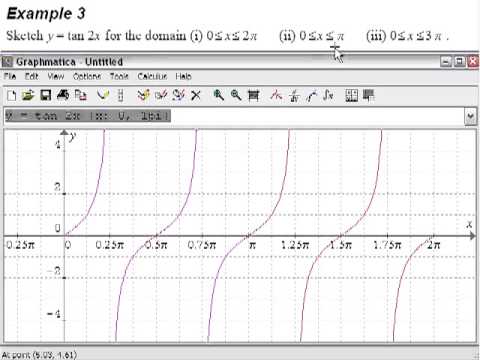
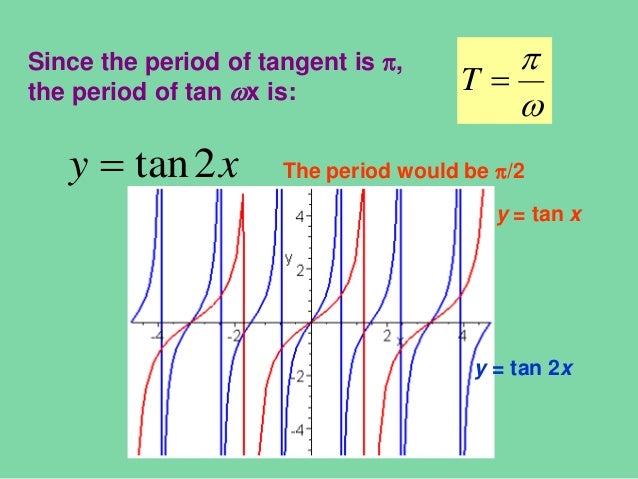
Trigonometry Graph Example 3 Sketch y = tan 2x Sketch the graph of y = tan 2x for (i) x= 0, 2pi, (ii) x= 0, pi, (iii) x= 0, 3piIf you like what you see, please subscribe toAs y = tan − 1 (tan x) is periodic with period π ∴ to draw this graph we should draw the graph for one interval π and repeat for entire values of x As we know;Gráfico y=tan(2x) Hallar las asíntotas Toca para ver más pasos Para cualquier , las asíntotas verticales existen en , donde , es un número entero Use el periodo básico para , , para encontrar la asíntota vertical de


How Do You Graph Ytan 2x Class 11 Maths Cbse


Graphs Of Trigonometric Functions
2 π that has length πSo its, graph could be plotted asYou can put this solution on YOUR website!22/5/18Please Subscribe here, thank you!!!


Trigonometric Graphs And Transformations Tan And Cot


Graphing Tangent Functions
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreTan Graph The tan function is completely different from sin and cos function The function here goes between negative and positive infinity, crossing through 0 over a period of π radian y = tan x;Graph y=3tan(2x) Equation of tan function y=Atan(BxC), period=π/B, phase shift=C/B, A is a multiplier that stretches the curve vertically
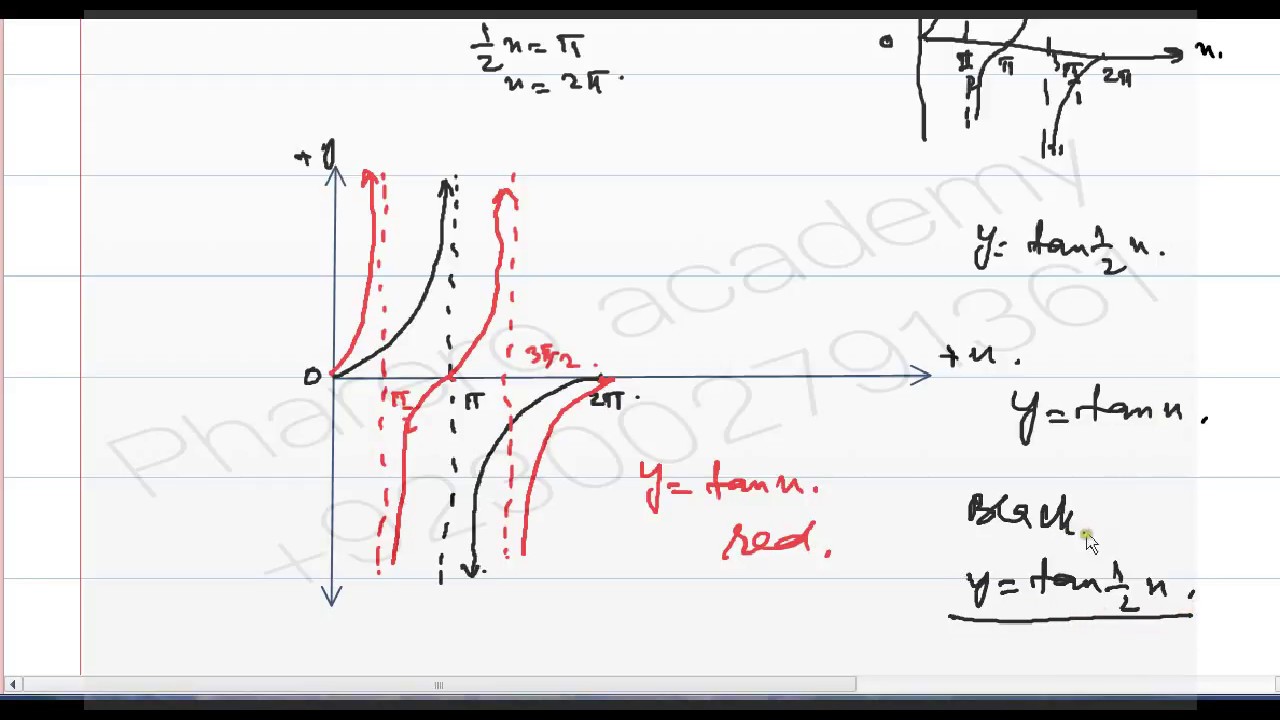


Graph Of Y Tan 1 2 X In Urdu Hindi Youtube


Solution Graph One Complete Cycle Of Y 1 Tan 2x Pi 4
Trigonometry The graphs of tan and cotIn this graph, the cosine curve is shown in gray, and the secant curve in blue y = cos x (in gray) and y = sec x (in blue) One more step we need the square of the secant graph values that is, we are going to graph y = sec 2 x To do that, we just take each yvalue of the secant curve and square it So for example the point (105, 2) on the y = sec x curve becomes (105, 4) on the19/3/18Assuming you know what ), the function is squished along the xaxis by a So, a= represents all the xvalues being doubled So if for a function f(x), f(2)=5 and f(4)=12, with f(x/2) f(4)=5 So, y=tan(x/2) would be y=tanx but each value of x would be doubled y=tanx graph{tanx 10, 10, 5, 5} y=tan(x/2)# graph{tan



Graphing Tangent Read Trigonometry Ck 12 Foundation


Solution Determine The Period Of Y Tan 2x
The cotangent graph has vertical asymptotes at each value of x where latex\tan x=0/latex;Sketch the graph of y = 5 sin 2xSee below The graph of y=tan3x is the graph of y=tanx with a horizontal compression by a factor of 1/3 The period of tanx is pi, so the period of tan3x is 1/3*pi=pi/3 Graphs
.png)


Sketch The Graph Of The Following Function On The Same Scale 10 Y Tan 2x Y Maths Meritnation Com



Tangent Graph
/3/18About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &Tan^2x1=0 full pad »Tan θ= 0 when θ= 0˚, 180˚, 360˚ tan θ = 1 when θ= 45˚ and 225˚ tan θ = –1 when θ= 135˚ and 315˚


Graph Tangent And Cotangent
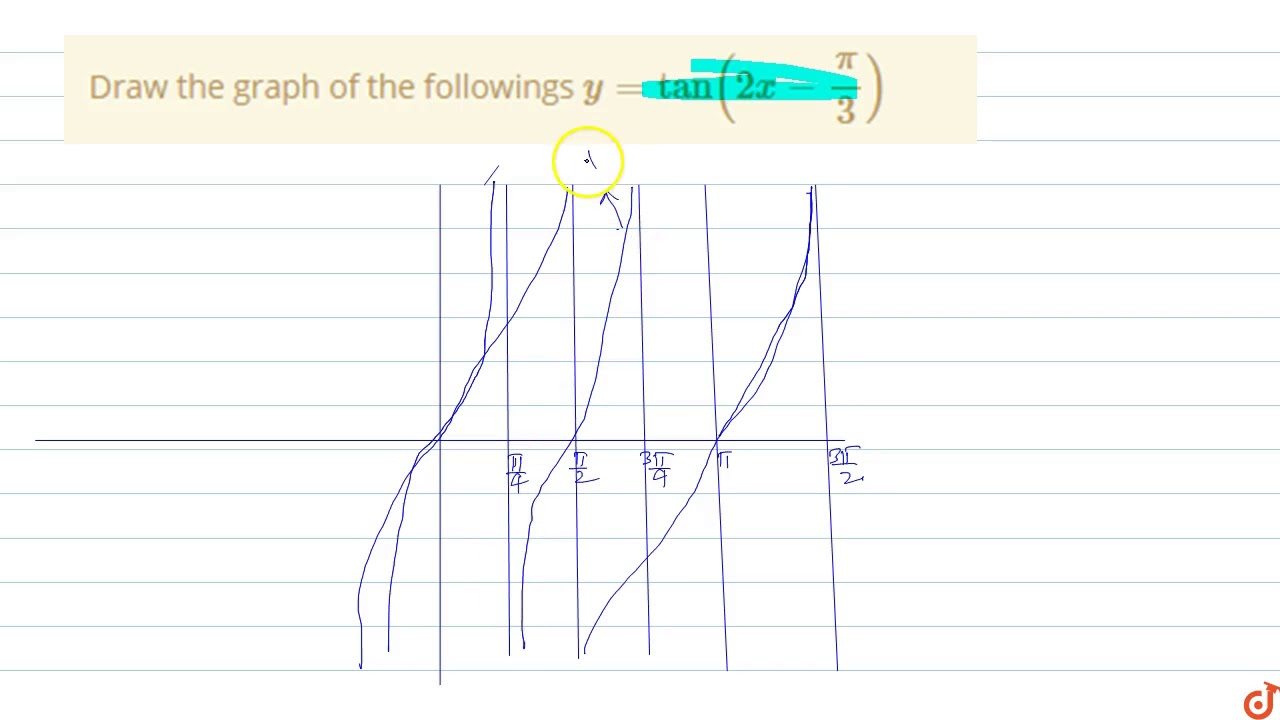


Draw The Graph Of The Followings Y Tan 2x Pi 3 Youtube
Knowledgebase, relied on by millions of students &21/6/07tan(x) = 1 everywhere sin(x) = cos(x) This is at pi/4 and every pi after that Draw a few of those It is zero everywhere sin(x) = 0 That's x = 0 and every pi after that Draw a few of those You should be seeing the shape of the thing Sketch a few periods y = 2tan(x) This is just a little vertical stretching Start with the graphSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more


Warm Upnov 25 Th Determine Whether To Us The Law Of Sine Or Cosine And Solve For The Missing Pieces 1 D Abc With A 12 B 13 C 24 2 D Abc Ppt Download


Graphs Of Tangent Cotangent Ppt Video Online Download
Solution for Graph the function 18) y = tan 2xSketch the graph of y = tan(2x π/2) over one period Solution Graphing Parameters range We start by skeching tan(2 x) over one period from 0 to π/2 (blue graph below) We then sketch y = tan 2( x π/4) translating the previous graph π/4 to the left (red graph below) so that the sketched period starts at π/4 and ends at14/4/162 tanx 1 − tan2x = 2 sinx cosx 1 − ( sin2x cos2x) = 2sinx cosx cos2x −sin2x = sin2x cos2x = tan2x Proofs for sin2x = 2sinxcosx and cos2x = 1 −2sin2x Use Area of a ABC = 1/2 (base) (altitude) = 1/2 bc sin A Here, it is the ABC of a unit circle, with center at A, B and C on the circle and ∠ A = 2x


6 Trigonometry Graph Example 3 Sketch Y Tan 2x Youtube



Tangent Cotangent Secant And Cosecant Graphs Mathbitsnotebook Ccss Math
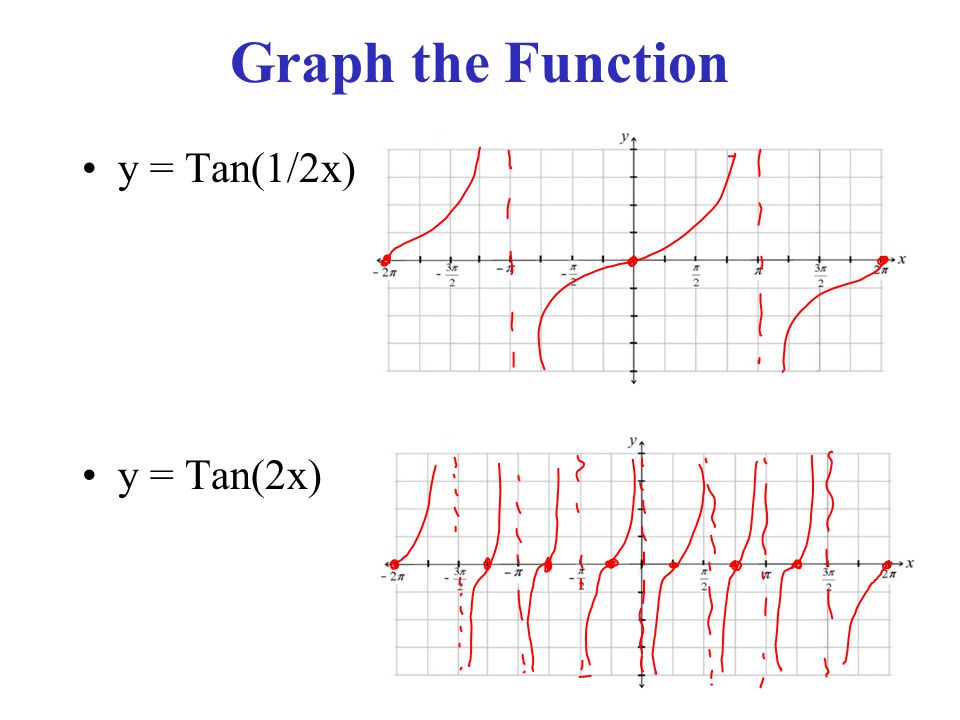
Tan ( x) − 2 x = 0, x ∈ ( − π / 2, π / 2) So far I've tried adding 2 x to both sides and doing some manipulations, but I can't seem to isolate the x (and I'm not even sure if that's what I have to do here) I guess in the worst case scenario I could always just graph y = tan 15/4/184 Graphs of tan, cot, sec and csc by M Bourne The graphs of `tan x`, `cot x`, `sec x` and `csc x` are not as common as the sine and cosine curves that we met earlier in this chapter However, they do occur in engineering and science problemsFind the asymptotes Tap for more steps For any y = tan ( x) y = tan ( x), vertical asymptotes occur at x = π 2 n π x = π 2 n π, where n n is an integer Use the basic period for y = tan ( x) y = tan ( x), ( − π 2, π 2) ( π 2, π 2), to find the vertical asymptotes for y = tan ( x 2) y = tan ( x 2)



Tangent Graphs Worked Solutions Examples Videos



The Tangent Function Functions Siyavula
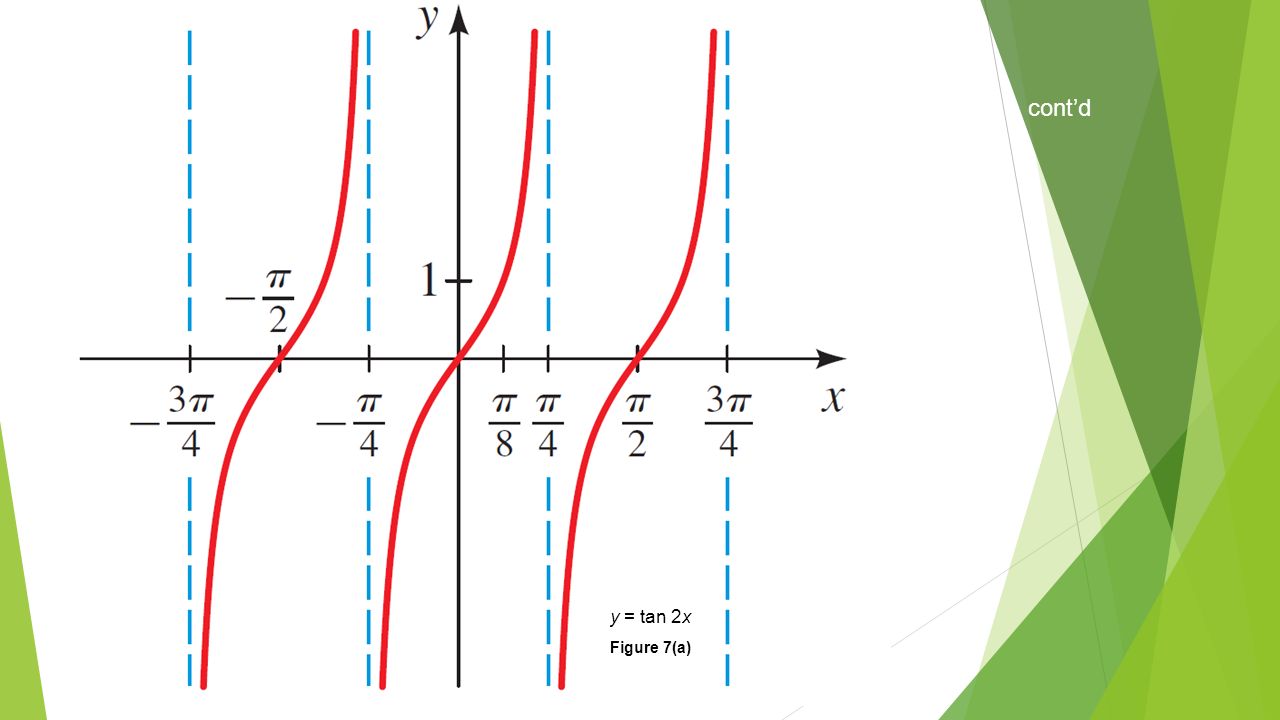
The graph of y = tan θ, for 0˚ ≤ θ ≤ 360˚ obtained is as shown Properties of the tangent function The curve is not continuous It breaks at θ = 90˚ and 270˚, where the function is undefined ;The period of the graph \(y = \tan{x}\) is 180°//googl/JQ8NysSketch the Graph of f(x) = tan(2x)


Tan Graph



01 Ex13 Sketch Y Tan 2x 1 Youtube
Compute answers using Wolfram's breakthrough technology &Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes0 ⇒ f goes down x ∈ (0, π 2) ⇔ f '(x) >


Graph Tangent And Cotangent



Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Video Online Download
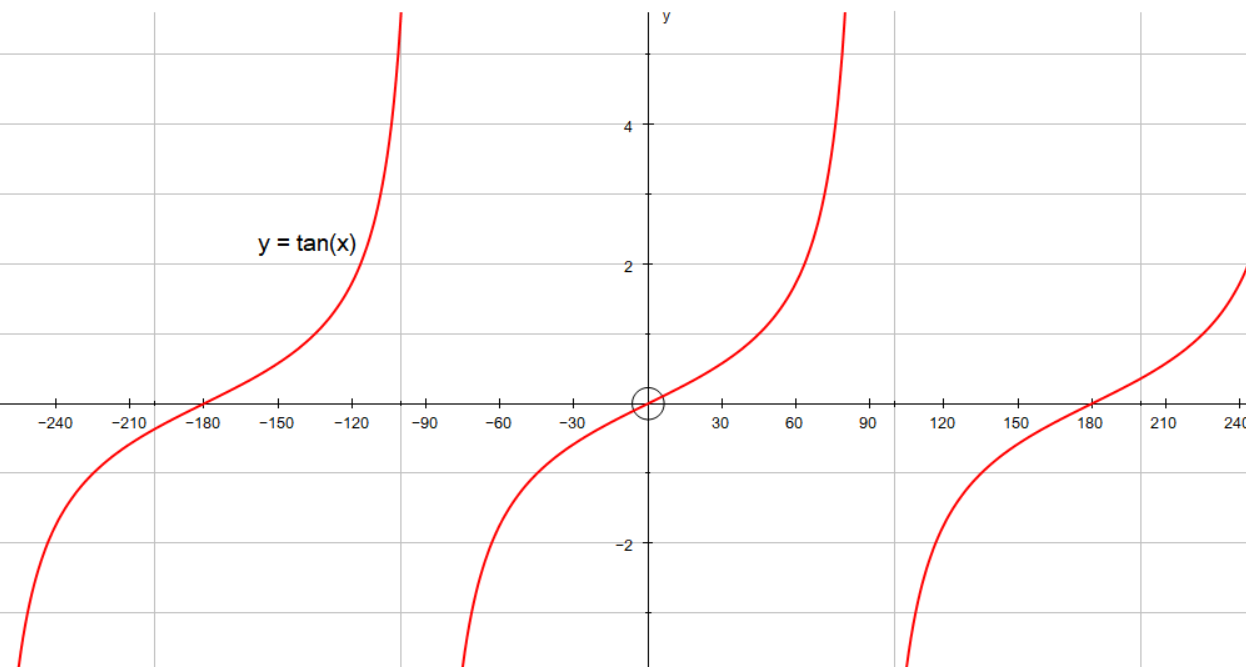
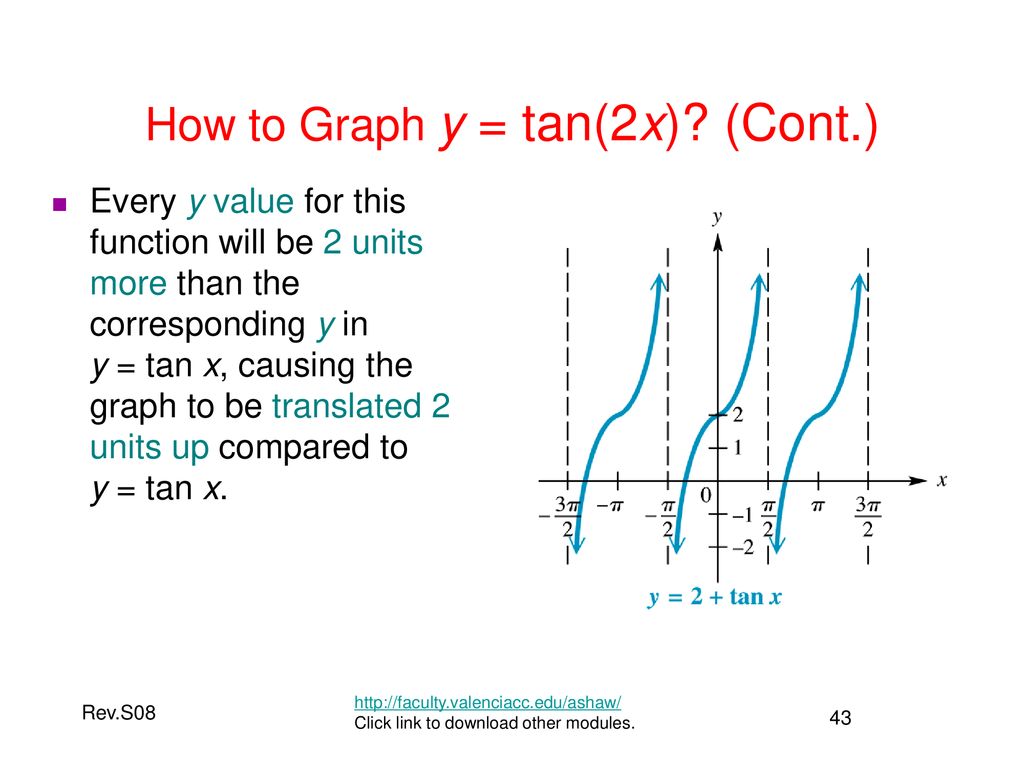
\(x\) = 60°, 240°, 4°X = π 4 x = π 4 The basic period for y = tan ( 2 x) y = tan ( 2 x) will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a number and zero The distance between 0 0 and 2 2 is 2 2 π 2 π 2Analyzing the Graph of \(y =\tan x\) We will begin with the graph of the tangent function, plotting points as we did for the sine and cosine functions Recall that \\tan \, x=\dfrac{\sin \, x}{\cos \, x} \nonumber\ The period of the tangent function is \(\pi\) because the graph repeats itself on intervals of \(k\pi\) where \(k\) is a constant


How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic


Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints
So to calculate the other solutions add 180°Hope, its enough to understand26/7/Revise the relationship between trigonometric formula and graphs as part of National 5 Maths Homepage Accessibility links What is the period of a graph with the equation \(y = \tan 2x


Draw The Graph Of Y Tan 2 X


Draw The Graph Of Y Tan 1 2x 1 X 2
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThe cotangent graph has vertical asymptotes at each value of x where latex\tan x=0/latex;X = π 2 x = π 2 The basic period for y = tan ( 2 x − π 2) y = tan ( 2 x π 2) will occur at ( 0, π 2) ( 0, π 2), where 0 0 and π 2 π 2 are vertical asymptotes ( 0, π 2) ( 0, π 2) The absolute value is the distance between a number and zero The distance between 0 0 and 2 2 is 2 2 π 2 π 2


Trigonometry Functions User S Blog


Graphing Tangent Functions
Le graphe de la fonction montre la courbe de la fonction mathématique suivante TAN(x)0 ⇒ f goes upSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more


4 Graphs Of Tan Cot Sec And Csc


Graphs Of Trigonometric Functions Symmetry With Respect To
The graph of \(y=\tan x\) does not have an amplitude, but we can see any vertical stretch by comparing the function values at the guidepoints Example 712 Graph \(y=13\tan 2x\text{}\) Describe the transformations of the graph, compared to \(y=\tan x\text{}\)We show these in the graph below with dashed lines Since the cotangent is the reciprocal of the tangent, latex\cot x/latex has vertical asymptotes at all values of x where latex\tan x=0/latex , and latex\cot x=0/latex at all values of x where tan x has its vertical asymptotes28/6/14so what I hope to do in this video is get some familiarity with the graph of tangent tangent of theta and to do that I'll set up a little unit circle so that we can visualize what the tangent of various Thetas are so let's say that's a yaxis this is my xaxis that is my xaxis and the unit circle would look something something like this and we already know this is all of a refresher of the


Review Cocalc
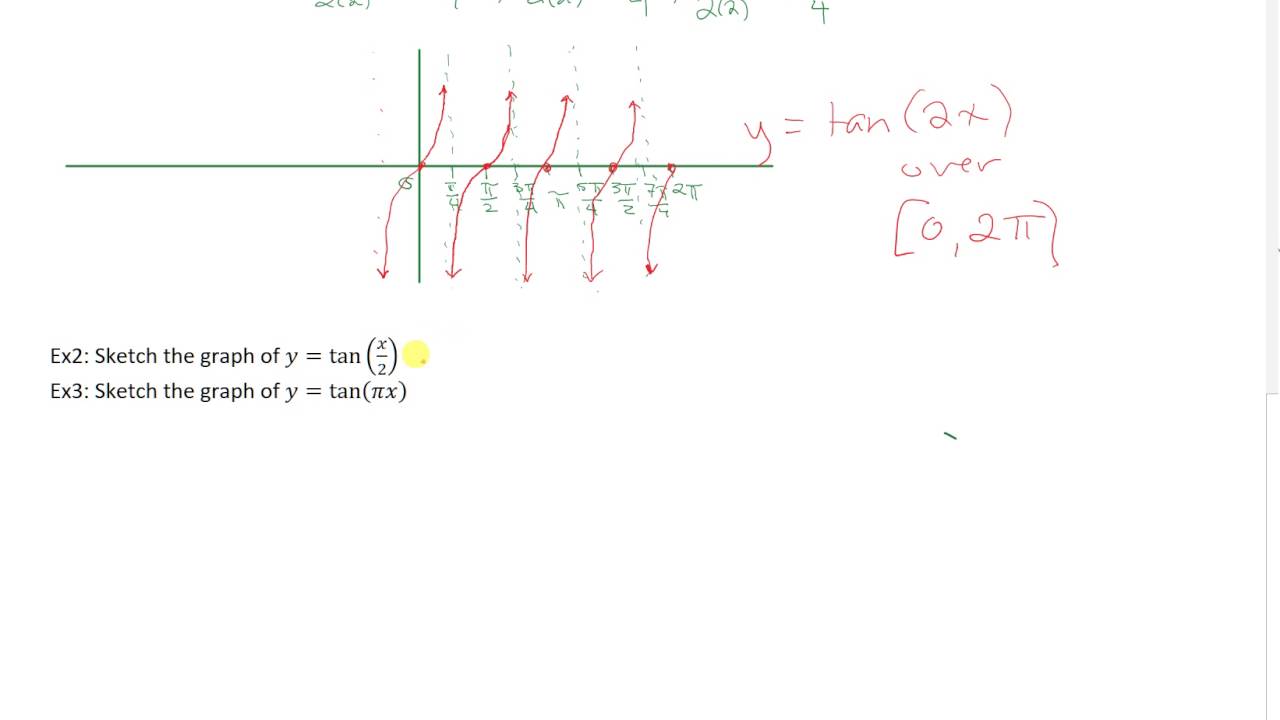


Sketching Y Tan 2x And Y Tan X 2 Youtube
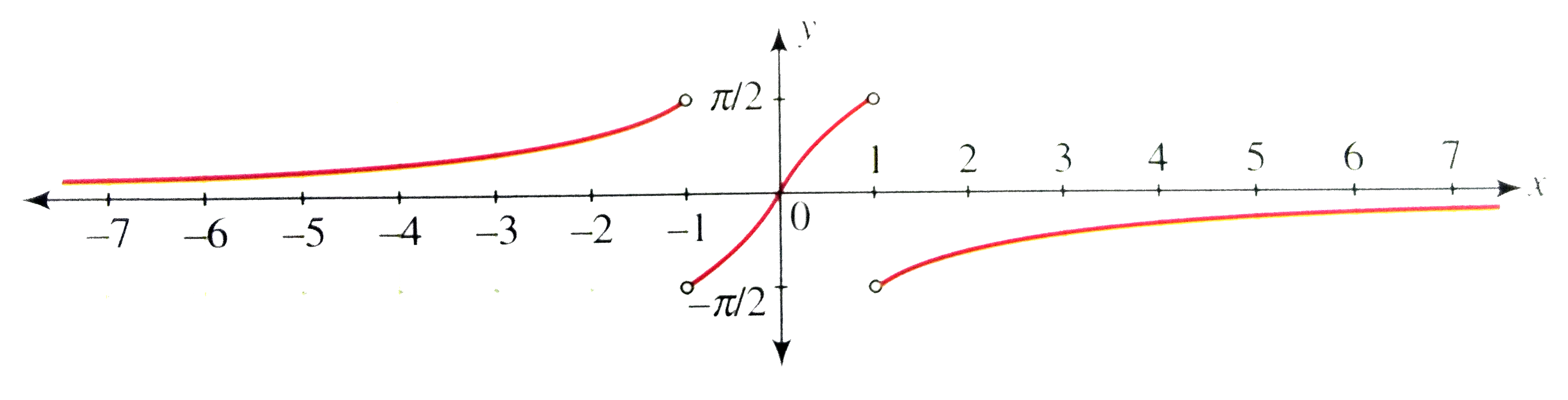
Prove that the general solution of tan θ = tan ∝ is given by θ = nπ ∝, n ∈ Z Solution We have, tan θ = tan ∝ ⇒ sin θ/cos θ sin ∝/cos ∝ = 0 ⇒ (sin θ cos ∝ cos θ sin ∝)/cos θ cos ∝ = 0 ⇒ What is the derivative of cos^1 (2x (1x^2)^ (1/2)) and tan^1 ( (4x^1/2)/ (14x))?Y = tan − 1 (tan x) = {x − 2 π <Safety How works Test new features Press Copyright Contact us Creators
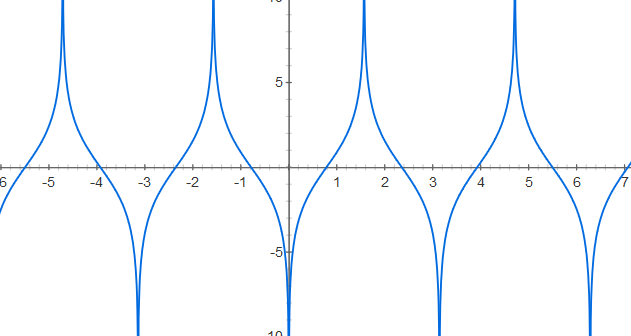


How Do You Graph Y Ln Tan 2 X Socratic


Graphs Of Other Trigonometric Functions Ppt Video Online Download
3/5/21Solution for Sketch the graph y= tan(2x) y 3= Find the period, asymptotes, and interceptsSee below tanx has a period of pi tan(pi/3) is tanx with a horizontal stretch by a factor of 3 This makes the period pi *3=3pi, so for 2 periods is 6pi This can be seen from the graphsYou will learn almost everything for tan graph from basic to advance in this video It is very useful for Modern Maths or Add Maths students in SPM In this



Tangent And Cotangent Graphs Ck 12 Foundation



Solved Sketch The Graph Of The Following Functions Y Tan 2x Y Self Study 365



Tan Graphs Circular Functions
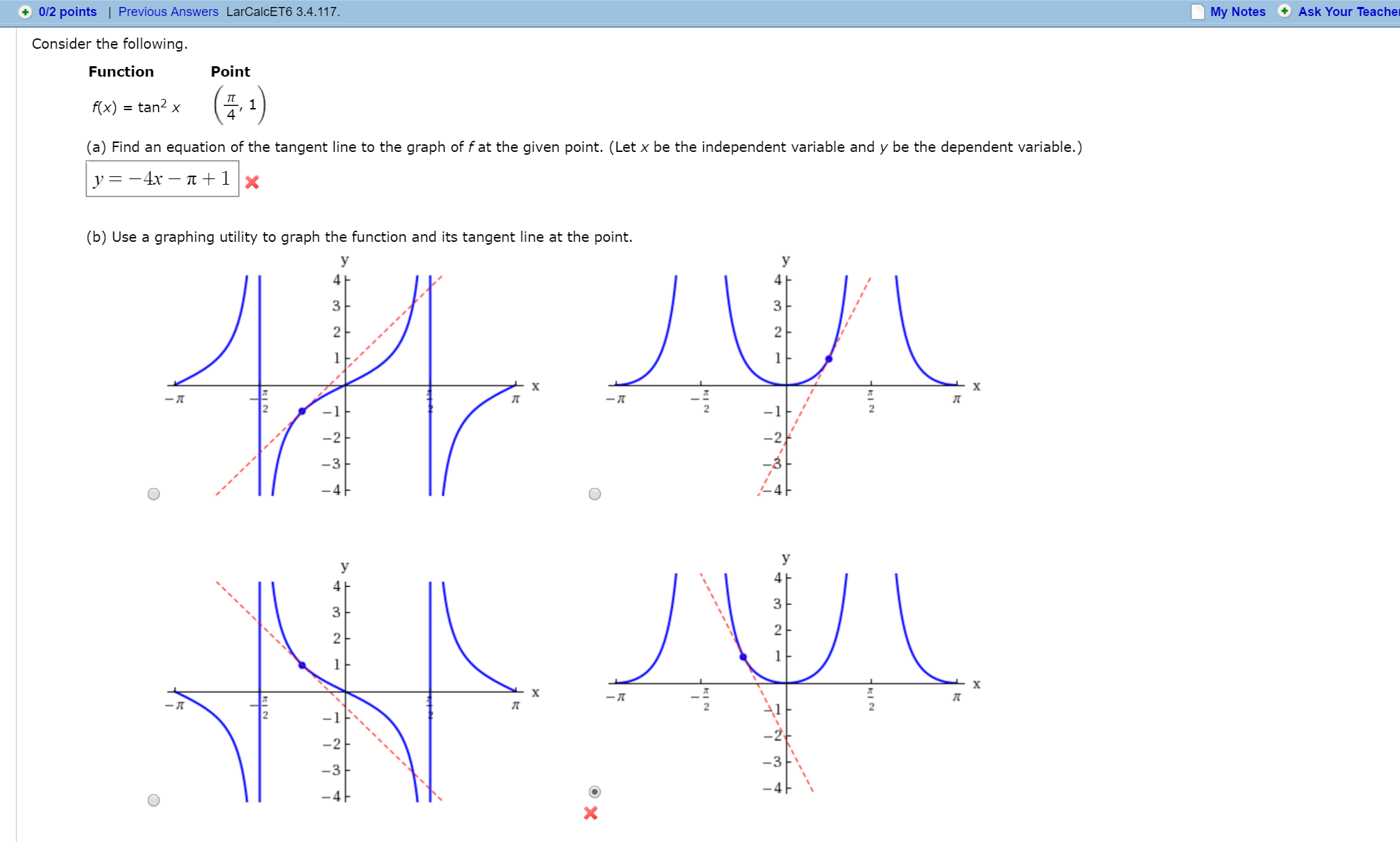


Solved Consider The Following Function F X Tan 2 X Poi Chegg Com


Long Question 3 User S Blog


What Is The Period Of This Function Sin4x Tan2x Quora
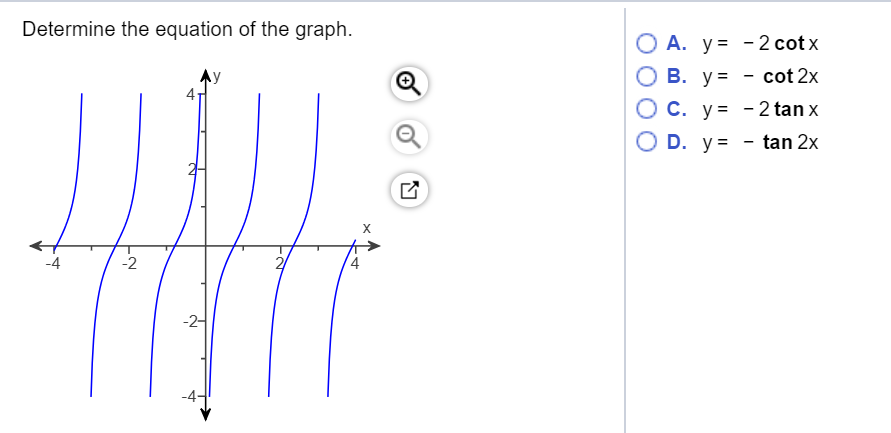


Solved Determine The Equation Of The Graph 2 Cotx Ov U Chegg Com


Derivative Of Tan X


How Do You Graph Y Tan3x Socratic



The Tangent Function Functions Siyavula


Find The Period Of Tan 2x Class 10 Maths Cbse



Solved Sketch The Graph Of The Function Include Two Ful Chegg Com



Graphing The Tangent Function Amplitude Period Phase Shift Vertical Shift Video Lesson Transcript Study Com
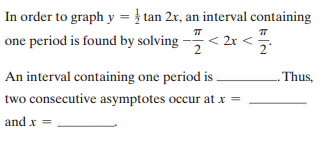


Answered In Order To Graph Y Tan 2x An Bartleby


Graph Tangent And Cotangent



Find The Roots Of The Function Mathematics Stack Exchange
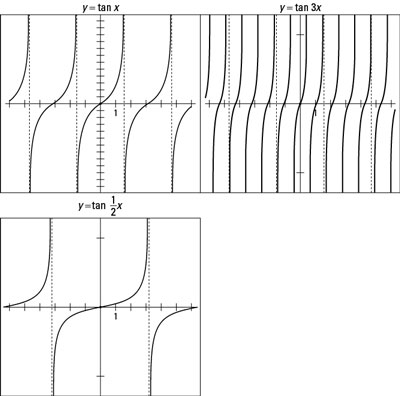


Graph Tangent Functions With Variable Multipliers Dummies



Trig Transformations Of Graphs



Sketch The Graph 1 Y Cos 2 X 2 Y Tan2x 3 Y Sin2x Maths Trigonometric Functions Meritnation Com



Tangent Graph


Biomath Trigonometric Functions


Answered Graph The Function 18 Y Tan 2x Bartleby
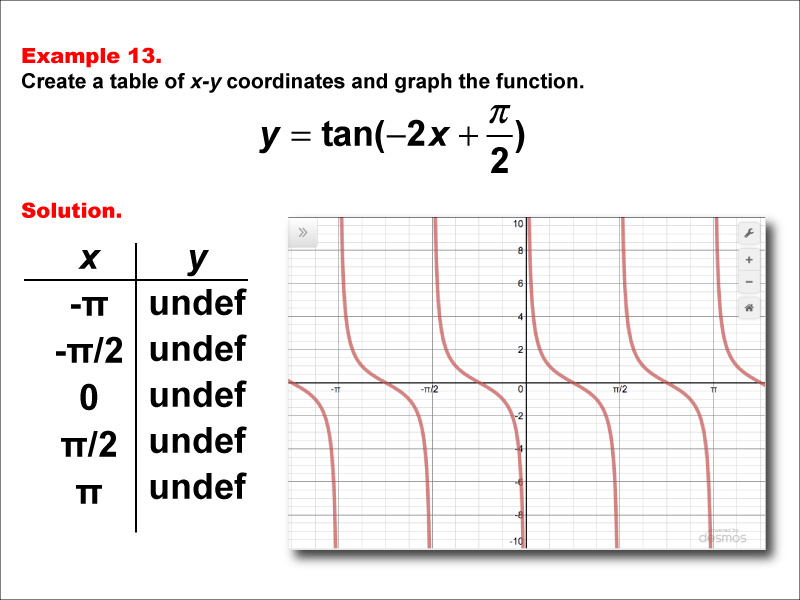


Math Example Tangent Functions In Tabular And Graph Form Example 13 Media4math



Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube


Graphing Tangent Functions
.png)


Sketch The Graphs Of The Following Functions 4 Y Tan 2x Math Meritnation Com



Solved Graph The Function Over One Period Interval Y Ta Chegg Com


Graphs Of The Tangent And Cotangent Functions


Solution Graph Y 1 2 Tan 2x Pi 2 And The Period And Phase Shift
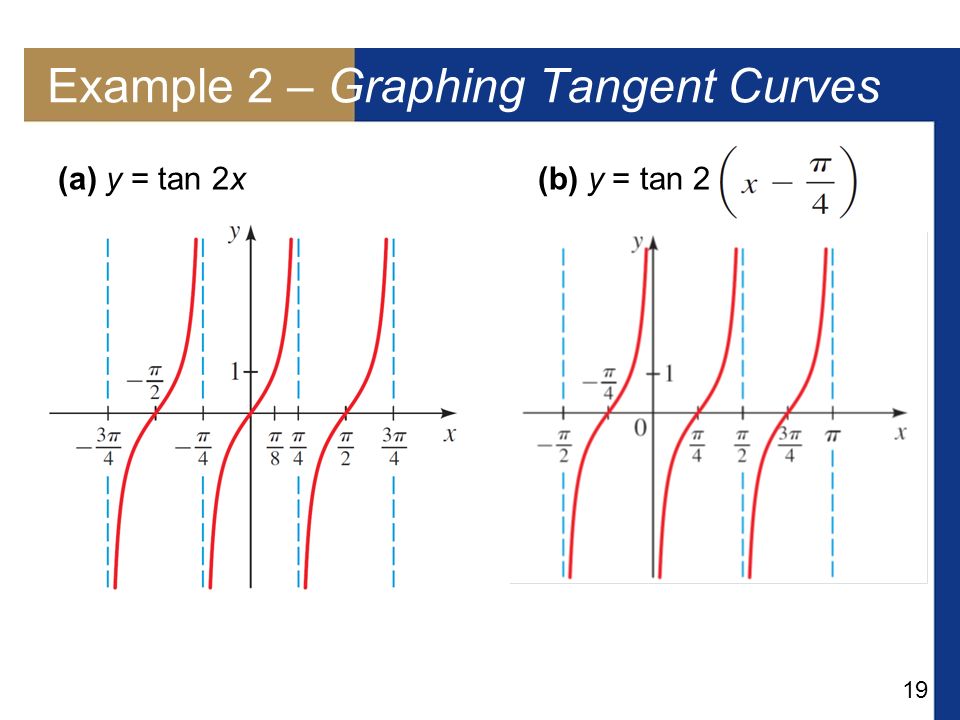


More Trigonometric Graphs Ppt Download


Solution Y 2 Tan 2x Graph Two Periods Of The Given Tangent Function
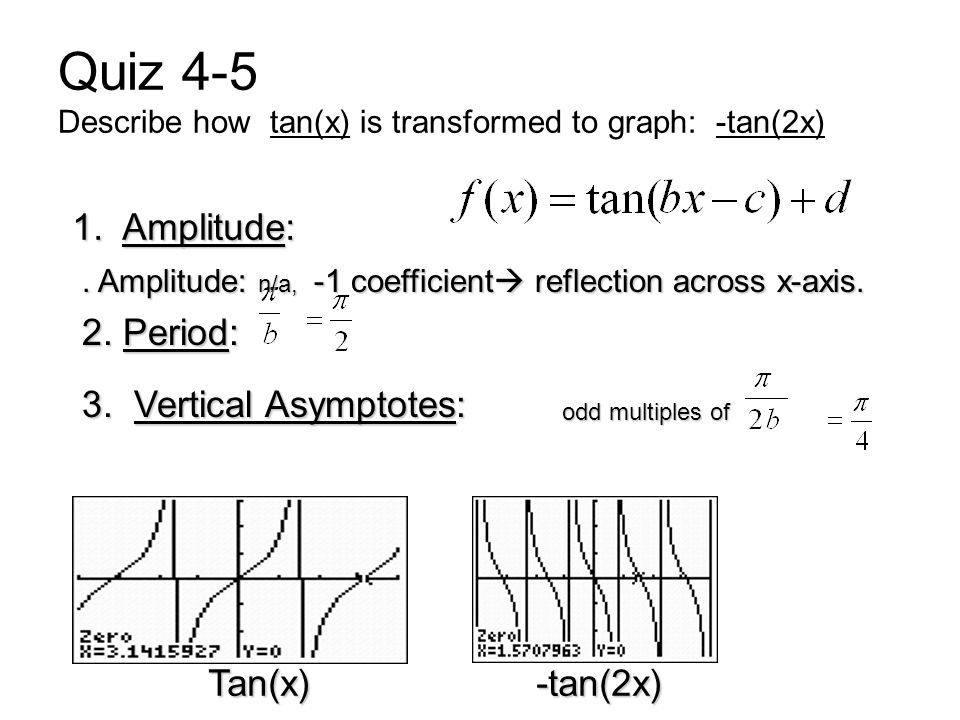


Quiz 4 5 Describe How Tan X Is Transformed To Graph Tan 2x Ppt Download


Tangent Graphs Worked Solutions Examples Videos


Tangent Graphs Worked Solutions Examples Videos



Ex 6 3 Q10 F X Tan 2x Sketch The Graphs Of The Following Functions


4 Graphs Of Tan Cot Sec And Csc
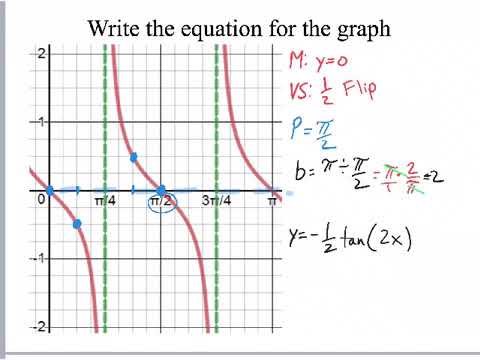


Writing Equations For Tangent Graphs Youtube


Howto How To Find Vertical Asymptotes Of Tan2x
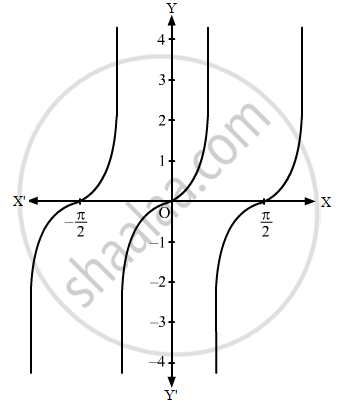


Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com


Content Graphing The Trigonometric Functions
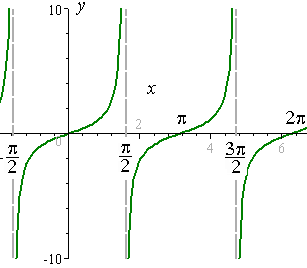


4 Graphs Of Tan Cot Sec And Csc
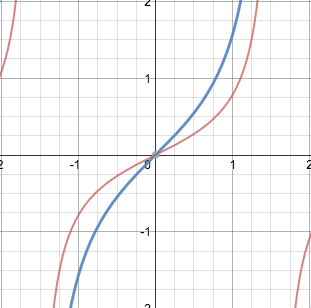


What Is The Graph Of Y 1 2 Tan X Socratic
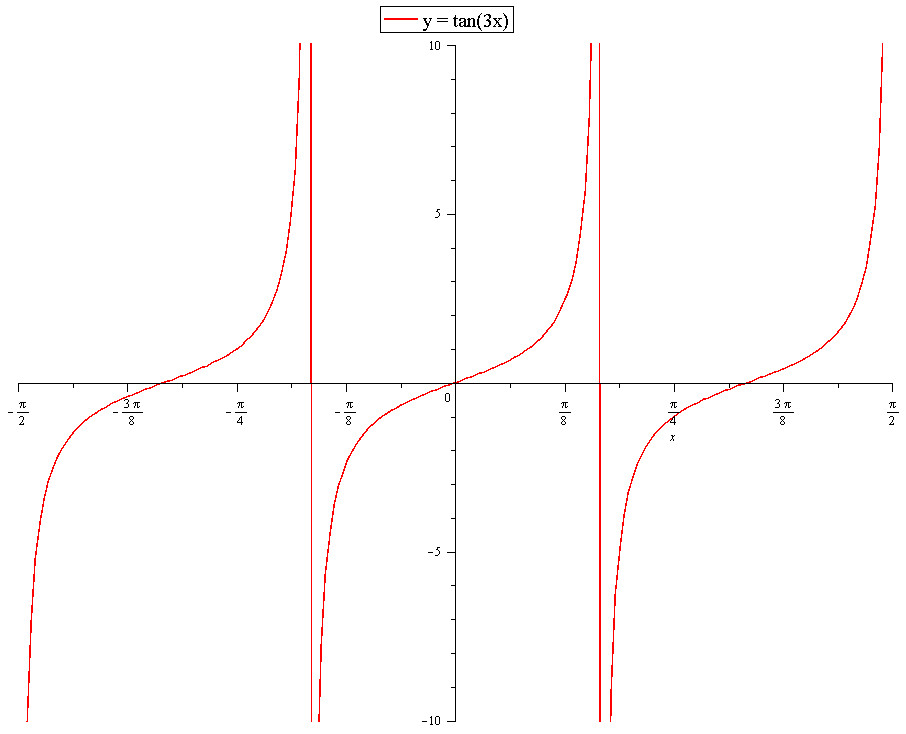


How Do You Graph Y Tan3x Socratic


Howto How To Find Vertical Asymptotes Of Tan2x Cute766



Graphing Tangent Read Trigonometry Ck 12 Foundation
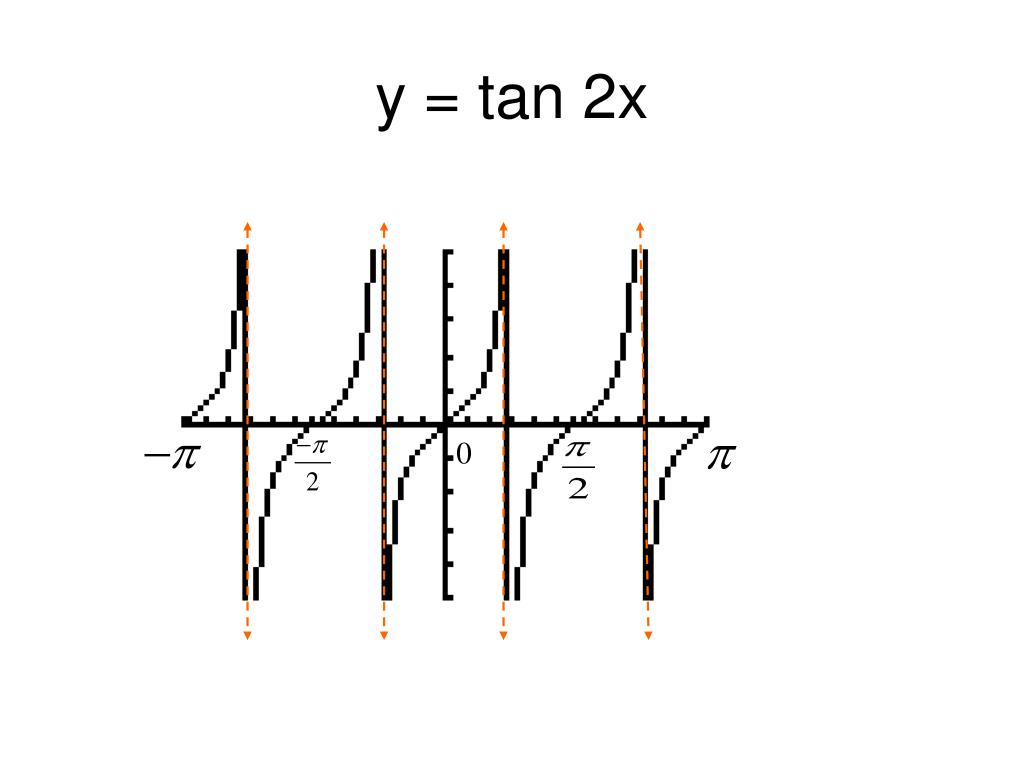


Ppt Graphing Tangent Powerpoint Presentation Free Download Id
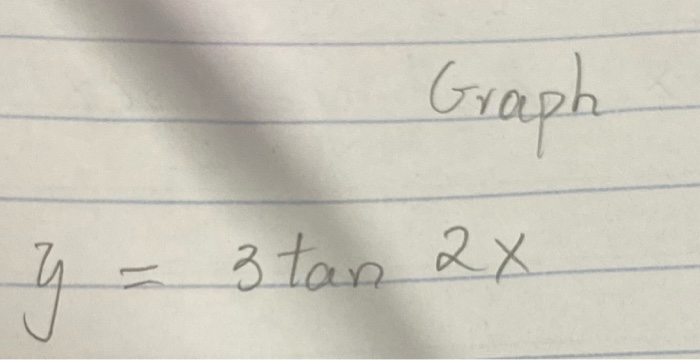


Solved Graph Y 3 Tan 2x Chegg Com


What Is The Graph Of Mod Of Tan X Quora



Sketch The Graph Of The Tangent Curve Y Tan 2x In The Interval From 0 To 2pi Brainly Com


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3



How To Graph Tan Ex Y Tan2x Study Com



Solved Graph The Function Show At Least Two Periods On T Chegg Com


Graph Tangent And Cotangent
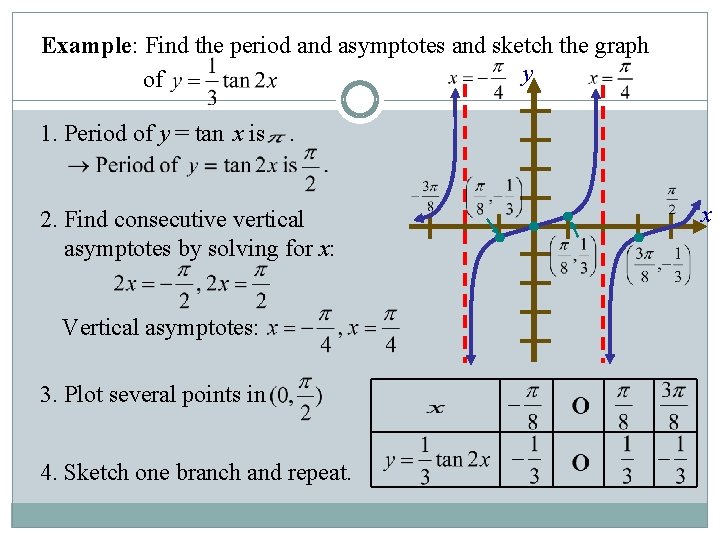


Unit 7 Trigonometric Functions Graphing The Trigonometric Function


Bestmaths



On Which Interval Is The Tangent Function Invertible Mathematics Stack Exchange


Sketch The Graph Of F X Tan 2x Youtube



Graphing Transformations Of Tangent Functions Flashcards Quizlet



Graphing Tangent Read Trigonometry Ck 12 Foundation


Graphs Of Other Trigonometric Functions Lecture


Graphs Of The Circular Functions Ppt Download


Graphs Of The Other Trigonometric Functions Precalculus Ii
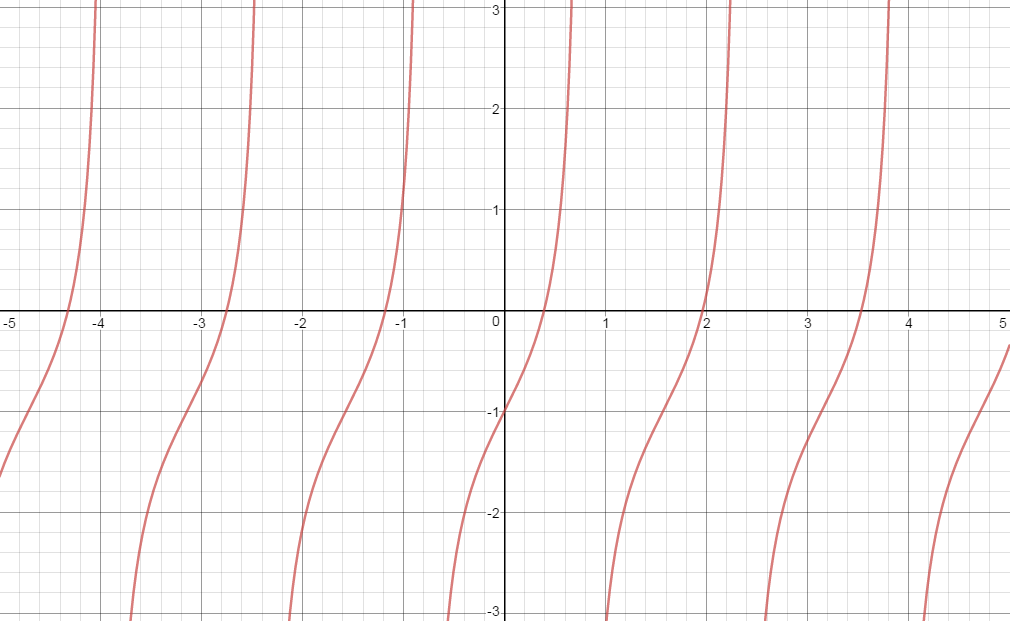


How Do You Graph Y 1 Tan2x Socratic



0 件のコメント:
コメントを投稿